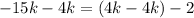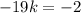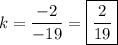Question

Solve this equation, and show work. worth 40 points.

Answer 1

Recall the following property of exponents:

`a^b\cdot a^c=a^(b+c)`

`\implies 216^(-3k)\cdot 216^(-2k)=216^(-3k-2k)=216^(-5k)`

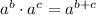
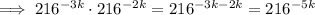
Now, notice that 6² = 36 and 6³ = 216, which means that

`216^(-5k)=36^(2k-1) \iff (6^3)^(-5k)=(6^2)^(2k-1)`

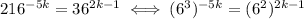
Recall another property of (real) exponents:

`(a^b)^c=a^(bc)`

`\implies(6^3)^(-5k)=6^(3(-5k))=6^(-15k)\text{ and }(6^2)^(2k-1)=6^(2(2k-1))=6^(4k-2)`

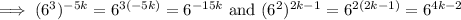
So we have

`216^(-5k)=36^(2k-1) \iff 6^(-15k)=6^(4k-2)`

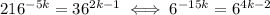
Since both sides are equal powers of 6, that must mean that the exponents must be equal, so

`-15k=4k-2`

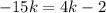
Solve for k :

`-15k-4k=(4k-4k)-2`

`-19k=-2`

`k=(-2)/(-19)=\boxed{\frac2{19}}`