Answer:
D
Explanation:
From the triangle inequality, we know that the two small sides must be greater than the largest side. Let's let x be the third side:
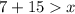
However, 15 can also be our largest side. So:
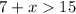
Let's solve for x for both inequalities.
First inequality:
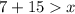
Add:
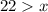
Flip:
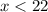
Second inequality:
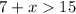
Subtract 7 from both sides:
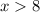
So, we have the compound inequality:
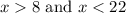
Combine:
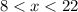
Our answer is D
And we're done!