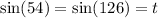Question

Please just explain/show how to set up #1. I want to do the work on my own

and please someone check my work on 2 and 3
please hurry this is due in an hour and a half

Answer 1

See below.

Explanation:

We have:

`(\sqrt3)/(\sin(\theta))=2`

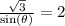
And we want to find two different angles between 0 and 180 that satisfy this equation.

First, let's get our sine out of the denominator. Notice that this is the same as:

`(\sqrt3)/(\sin(\theta))=(2)/(1)`

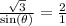
Cross-multiply:

`2\sin(\theta)=√(3)`

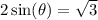
Divide both sides by 2:

`\sin(\theta)=(√(3))/(2)`

Here you go! I'll have the answer for you if you scroll down, so check it when you're ready!

#2 is correct. However, double check #3. The answer's down there too... :)

[Blank space...]

[More blank space...]

[And more...]

Answer for 1)

We have:

`\sin(\theta)=√(3)/2`

So, at what points between 0 and 180 does sine equal √3/2?

If we refer to the unit circle, we can see that this happens twice: at 60.

Thus, the second time it occurs will be at 180-60 or 120.

So:

`\theta=60\textdegree\text{ or } 120\textdegree`

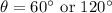
Answer for 3)

So you are correct for the first three. So:

`\sin(54)=t`

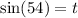
However, sine stays positive. So, our angle must be between 0 and 180.

So, instead of 180+54, it should be 180-54, giving us:

`\sin(54)=\sin(126)=t`