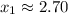Question

Solve using the Quadratic Formula. 3x2 - 7x - 3 = 0

Answer 1

`\displaystyle x_1=(7+ √(85))/(6)\approx 2.70\\\displaystyle x_2=(7- √(85))/(6)\approx -0.37`

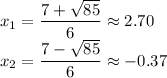
Explanation:

Quadratic Formula

Given the second-degree equation:

`ax^2+bx+c=0`

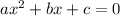
The solutions of the equation can be obtained by applying the formula:

`\displaystyle x=(-b\pm √(b^2-4ac))/(2a)`

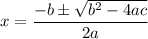
The equation to solve is:

`3x^2-7x-3=0`

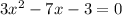
Which means the values of the coefficients are: a=3, b=-7, c=-3. Substituting the values in the formula:

`\displaystyle x=(-(-7)\pm √((-7)^2-4(3)(-3)))/(2(3))`

`\displaystyle x=(7\pm √(49+36))/(6)`

`\displaystyle x=(7\pm √(85))/(6)`

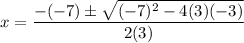
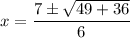
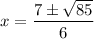
There are two real solutions for this equation:

`\displaystyle x_1=(7+ √(85))/(6)`

`\displaystyle x_2=(7- √(85))/(6)`

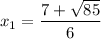
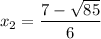
The approximate values of both roots are:

`x_1\approx 2.70`

`x_2\approx -0.37`