Question

Unit Test / 16 of 25

1 Pause
Josh practices free throws during basketball practice on Monday and Tuesday, On Monday, he attempts 15 free throws and 6 basketballs
went in the basket. Over both days, Josh wants at least 80% of his balls to go in the basket. If he makes every free throw on Tuesday,
what is the minimum number of free throws required on Tuesday to reach his goal?

Answer 1

30

Explanation:

For the minimum free throws, he must put every throw to the basket.

So, let n be the number of throws for Tuesday, in which all the throws are successful.

So, over both the days, total free throws he makes= 15+n.

Total numbers of throws that went in the basket= 6+n.

As he wants at least 80% of his balls to go in the basket.

So, 6+n is greater than or equal to 809% of 15+n, i.e

`6+n\geq (80)/(100)* (15+n)`

`\Rightarrow 30+5n\geq 60+4n`

`\Rightarrow n\geq 30.`

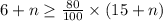
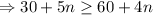
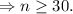
Hence, the minimum number of free throws required on Tuesday to reach his goal is 30.