Question

What is the relationship between area in the scale drawing and area on the on the actual tennis court if the scale is 1in.: 5ft. and the length of the scale is 15.6 and the width is 7.2 in.

What is the ratio of areaof the actual court to the area of the drawing (as a unit rate)? Is it the same as the ratio of length of the actual court to the length of the drawing?

Answer 1

Given:

Length of the scale = 15.6 in.

Width of the scale = 7.2 in.

Scale of drawing = 1 in. : 5ft.

To find:

The ratio of area of the actual court to the area of the drawing (as a unit rate).

And to check whether it is the same as the ratio of length of the actual court to the length of the drawing.

Explanation:

We have,

1 in. = 5ft.

Now, using this scale we get

15.6 in. = (15.6 × 5) ft =78 ft.

7.2 in. = (7.2 × 5) ft = 36 ft.

So, the actual length and width of tennis court are 78 ft and 36 ft respectively.

Area of actual tennis court is

`Area=length* width`

`Area=78* 36`

`Area=2808\text{ ft}^2`

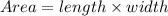
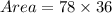
The area of drawing is

`Area=15.6* 7.2`

`Area=112.32\text{ in.}^2`

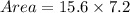
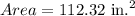
Now, ratio of area of the actual court to the area of the drawing (as a unit rate) is

`(2808)/(112.32)=(25)/(1)=25:1`

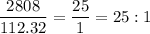
Ratio of area is 25:1 and ratio of length is 5:1 both area not same.

Therefore, the ratio of area of the actual court to the area of the drawing (as a unit rate) is 25:1.