Question

A proton travels through uniform magnetic and electric fields. The magnetic field is in the negative x direction and has a magnitude of 3.54 mT. At one instant the velocity of the proton is in the positive y direction and has a magnitude of 2230 m/s. At that instant, what is the magnitude of the net force acting on the proton if the electric field is (a) in the positive z direction and has a magnitude of 5.25 V/m, (b) in the negative z direction and has a magnitude of 5.25 V/m, and (c) in the positive x direction and has a magnitude of 5.25 V/m

Answer 1

(a). The magnitude of the net force is
`(2.1*10^(-18)\ N)k`

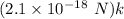
(b). The magnitude of the net force is
`(4.23*10^(-19)\ N)k`

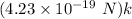
(c). The magnitude of the net force is
`(8.4*10^(-19)\ N)i+(12.6*10^(-19)\ N)k`

Step-by-step explanation:

Given that,

Magnetic field
`B=-3.54*10^(-3)i\ T`

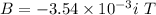
Velocity = 2230j m/s

We know that,

The net force acting on the proton is equal to the sum of electric and magnetic force.

`F=F_(e)+F_(B)`

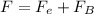
(a). If the electric field is in the positive z direction and has a magnitude of 5.25 V/m,

We need to calculate the magnitude of the net force acting on the proton

Using formula of net force

`F_(net)=e(E+v* B)`

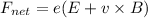
Put the value into the formula

`F_(net)=1.6*10^(-19)(5.25k+2230*-3.54*10^(-3)(j* i))`

`F_(net)=1.6*10^(-19)(5.25k+2230*-3.54*10^(-3)(-k))`

`F_(net)=(2.1*10^(-18)\ N)k`

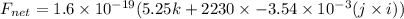
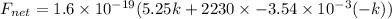
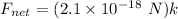
(b). If the electric field is in the negative z direction and has a magnitude of 5.25 V/m,

We need to calculate the magnitude of the net force acting on the proton

Using formula of net force

`F_(net)=e(E+v* B)`

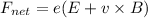
Put the value into the formula

`F_(net)=1.6*10^(-19)(-5.25k+2230*-3.54*10^(-3)(j* i))`

`F_(net)=1.6*10^(-19)(-5.25k+2230*-3.54*10^(-3)(-k))`

`F_(net)=(4.23*10^(-19)\ N)k`

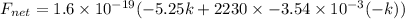
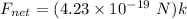
(c). If the electric field is in the positive x direction and has a magnitude of 5.25 V/m

We need to calculate the magnitude of the net force acting on the proton

Using formula of net force

`F_(net)=e(E+v* B)`

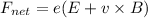
Put the value into the formula

`F_(net)=1.6*10^(-19)(5.25i+2230*-3.54*10^(-3)(j* i))`

`F_(net)=(8.4*10^(-19)\ N)i+(12.6*10^(-19)\ N)k`

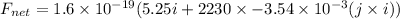
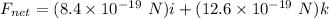
Hence, (a). The magnitude of the net force is
`(2.1*10^(-18)\ N)k`

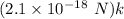
(b). The magnitude of the net force is
`(4.23*10^(-19)\ N)k`

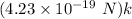
(c). The magnitude of the net force is
`(8.4*10^(-19)\ N)i+(12.6*10^(-19)\ N)k`