Question

Of the entering class at a​ college, ​% attended public high​ school, ​% attended private high​ school, and ​% were home schooled. Of those who attended public high​ school, ​% made the​ Dean's list, ​% of those who attended private high school made the​ Dean's list, and ​% of those who were home schooled made the​ Dean's list. A student is randomly chosen. ​a) Find the probability that the student made the​ Dean's list. ​b) Find the probability that the student ​, given that the student made the​ Dean's list. ​c) Find the probability that the student ​, given that the student did not make the​ Dean's list.

Answer 1

(a) The probability that the student made the​ Dean's list is 0.1655.

(b) The probability that the student came from a private high school, given that the student made the Dean's list is 0.2411.

(c) The probability that the student was not home schooled, given that the student did not make the Dean's list is 0.9185.

Explanation:

The complete question is:

Of the entering class at a college, 71% attended public high school, 21% attended private high school, and 8% were home schooled. Of those who attended public high school, 16% made the Dean's list, 19% of those who attended private high school made the Dean's list, and 15% of those who were home schooled made the Dean's list.

a) Find the probability that the student made the Dean's list.

b) Find the probability that the student came from a private high school, given that the student made the Dean's list.

c) Find the probability that the student was not home schooled, given that the student did not make the Dean's list.

Solution:

Denote the events as follows:

A = a student attended public high school

B = a student attended private high school

C = a student was home schooled

D = a student made the Dean's list

The provided information is as follows:

P (A) = 0.71

P (B) = 0.21

P (C) = 0.08

P (D|A) = 0.16

P (D|B) = 0.19

P (D|C) = 0.15

(a)

The law of total probability states that:

`P(X)=\sum\limits_(i) P(X|Y_(i))\cdot P(Y_(i))`

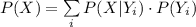
Compute the probability that the student made the​ Dean's list as follows:

`P(D)=P(D|A)P(A)+P(D|B)P(B)+P(D|C)P(C)`

`=(0.16* 0.71)+(0.19* 0.21)+(0.15* 0.08)\\=0.1136+0.0399+0.012\\=0.1655`

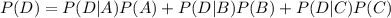
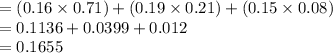
Thus, the probability that the student made the​ Dean's list is 0.1655.

(b)

Compute the probability that the student came from a private high school, given that the student made the Dean's list as follows:

`P(B|D)=(P(D|B)P(B))/(P(D))`

`=(0.21* 0.19)/(0.1655)\\\\=0.2410876\\\\\approx 0.2411`

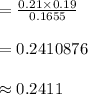
Thus, the probability that the student came from a private high school, given that the student made the Dean's list is 0.2411.

(c)

Compute the probability that the student was not home schooled, given that the student did not make the Dean's list as follows:

`P(C^(c)|D^(c))=1-P(C|D^(c))`

`=1-(P(D^(c)|C)P(C))/(P(D^(c)))\\\\=1-((1-P(D|C))* P(C))/(1-P(D))\\\\=1-((1-0.15)* 0.08)/((1-0.1655))\\\\=1-0.0815\\\\=0.9185`

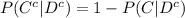
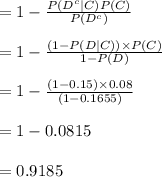
Thus, the probability that the student was not home schooled, given that the student did not make the Dean's list is 0.9185.