Question

LIKE 50-100 POINTS IDRK RIGHT ANSWERS ONLY OR I REPORT

What are the exact solutions of x2 − 3x − 7 = 0, where x equals negative b plus or minus the square root of b squared minus 4 times a times c all over 2 times a? x = the quantity of 3 plus or minus the square root of 37 all over 2 x = the quantity of negative 3 plus or minus the square root of 37 all over 2 x = the quantity of 3 plus or minus the square root of 19 all over 2 x = the quantity of negative 3 plus or minus the square root of 19 all over 2

Answer 1

The exact solution is:

x = the quantity of 3 plus or minus the square root of 37 all over 2

Explanation:

We are asked to find the exact solution of the polynomial equation which is given by:

`x^2 - 3x - 7 = 0`

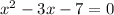
We know that the solution of the equation are the possible value of x which is obtained on solving the equation and hence satisfy the equation.

Now, on solving the quadratic equation i.e. degree 2 polynomial equation using the quadratic formula:

That is any polynomial equation of the type:

`ax^2+bx+c=0`

is solved by using the formula:

`x=(-b±√(x) b^2-4ac)/(2a)`

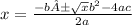
Here we have:

a=1, b=-3 and c=-7.

Hence, the solution of the equation is:

`x=(-(-3)±√((-3)^2-4*(-7)*1) )/(2*1)`

`x=(3±√(9+28) )/(2)`

`x=(3±√(37) )/(2)`

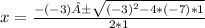
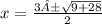
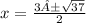
Hence, the solution is:

x = the quantity of 3 plus or minus the square root of 37 all over 2

( i.e.

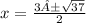`x=(3±√(37) )/(2)` )

Answer 2

x = the quantity of 3 plus or minus the square root of 37 all over 2

Explanation:

Given/To Find:

What are the exact solutions of x2 − 3x − 7 = 0, where x equals negative b plus or minus the square root of b squared minus 4 times a times c all over 2 times a?

Answer choices:

x = the quantity of 3 plus or minus the square root of 37 all over 2

x = the quantity of negative 3 plus or minus the square root of 37 all over 2 x = the quantity of 3 plus or minus the square root of 19 all over 2

x = the quantity of negative 3 plus or minus the square root of 19 all over 2

Solve:

By using the quadratic formula, the solutions are

`x=(-(-3)±√((-3)^2-4*1*(-7)))/(2*1)`

`x=(3±√(37))/(2)`

Hence, the answer is :

x = the quantity of 3 plus or minus the square root of 37 all over 2

Kavinsky