Question

g A population is infected with a certain infectious disease. It is known that 95% of the population has not contracted the disease. A test for this disease is 98% accurate (i.e., a person who has contracted the disease tests positive 98% of the time) and has a 1% false negative rate (i.e., a person without the disease has 1% positive rate). Find the probability that a random selected person from does not have the infection if he or she has tested positive. Briefly explain why you are or are not surprised by your result.

Answer 1

There is approximately 17% chance of a person not having a disease if he or she has tested positive.

Explanation:

Denote the events as follows:

D = a person has contracted the disease.

+ = a person tests positive

- = a person tests negative

The information provided is:

`P(D^(c))=0.95\\P(+|D) = 0.98\\P(+|D^(c))=0.01`

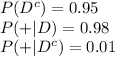
Compute the missing probabilities as follows:

`P(D) = 1- P(D^(c))=1-0.95=0.05\\\\P(-|D)=1-P(+|D)=1-0.98=0.02\\\\P(-|D^(c))=1-P(+|D^(c))=1-0.01=0.99`

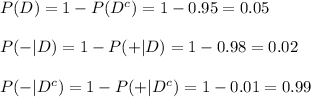
The Bayes' theorem states that the conditional probability of an event, say A provided that another event B has already occurred is:

`P(A|B)=(P(B|A)P(A))/(P(B|A)P(A)+P(B|A^(c))P(A^(c)))`

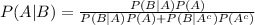
Compute the probability that a random selected person does not have the infection if he or she has tested positive as follows:

`P(D^(c)|+)=(P(+|D^(c))P(D^(c)))/(P(+|D^(c))P(D^(c))+P(+|D)P(D))`

`=((0.01* 0.95))/((0.01* 0.95)+(0.98* 0.05))\\\\=(0.0095)/(0.0095+0.0475)\\\\=0.1666667\\\\\approx 0.1667`

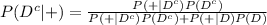
So, there is approximately 17% chance of a person not having a disease if he or she has tested positive.

As the false negative rate of the test is 1%, this probability is not unusual considering the huge number of test done.