Question

Suppose that 20% of the subscribers of a cable television company watch the shopping channel at least once a week. The cable company is trying to decide whether to replace this channel with a new local station. A survey of 100 subscribers will be undertaken. The cable company has decided to keep the shopping channel if the sample proportion is greater than 0.27. What is the approximate probability that the cable company will keep the shopping channel, even though the true proportion who watch it is only 0.20

Answer 1

There is approximately 4% chance that the cable company will keep the shopping channel, even though the true proportion who watch it is only 0.20.

Explanation:

The random variable X can be defined as the number of subscribers of a cable television company who watch the shopping channel at least once a week.

X follows a Binomial distribution with parameters n = 100 and p = 0.20.

But the sample selected is too large and the probability of success is close to 0.50.

So a Normal approximation to binomial can be applied to approximate the distribution of X if the following conditions are satisfied:

1. np ≥ 10

2. n(1 - p) ≥ 10

Check the conditions as follows:

`np=100* 0.20=20>10\\\\n(1-p)=100* 0.80=80>10`

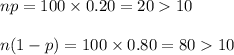
Thus, a Normal approximation to binomial can be applied.

`\hat p\sim N(p,(p(1-p))/(n))`

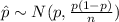
Compute the approximate probability that the cable company will keep the shopping channel, even though the true proportion who watch it is only 0.20 as follows:

`P(\hat p>0.27)=P(\frac{\hat p-p}{\sqrt{(p(1-p))/(n)}}>\frac{0.27-0.20}{\sqrt{(0.20(1-0.20)/(100)}})`

`=P(Z>1.75)\\=1-P(Z<1.75)\\=1-0.95994\\=0.04006\\\approx 0.04`

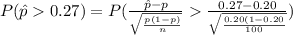
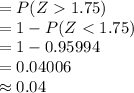
Thus, there is approximately 4% chance that the cable company will keep the shopping channel, even though the true proportion who watch it is only 0.20.