Question

16.4 A cylinder of water contains oxygen in solution. The cross- sectional area of the cylinder is 2 cm2 and the length of the cylin- der is 5 cm. At one end of the cylinder the concentration of oxygern is maintained at 0.2 mol m-3, this concentration falls linearly to 0.05 mol m-3 at the other end of the cylinder. The diffusion con- stant of oxygen in water is 8 × 10-10 m2 s-1. How many moles of oxygen pass down this cylinder every second? What mass of oxy- gen passes down the cylinder each second?

Answer 1

A) oxygen moles/sec = 48 * 10 ^-14 mol/sec

B) mass of oxygen = 1536*10^-14 grams

Step-by-step explanation:

cross sectional area of cylinder = 2cm^2 = 2 * 10^-4 m^2

length of cylinder = 5 cm = 0.05 m

concentration at one end = 0.2 mol m^-3

concentration falls linearly at other end = 0.05 mol m^-3

Diffusion constant of oxygen = 8 * 10^-10 m^2 s^-1

A ) Number of moles of oxygen passing every second

N = A * D *
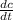`(dc)/(dt)` ------- ( 1 )

A = area , D = diffusion constant,
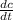`(dc)/(dt)` = rate of change of diffusion

dc /dt = ( 0.2 - 0.05 ) / 0.05 = 3 mol m^-4

back to the equation

N = ( 2 * 10^-4 ) * ( 8 * 10^-10 ) * ( 3 ) = 48 * 10 ^-14 mol/sec

B) Mass of oxygen passing down the cylinder each second

This can be obtained by converting : 48 * 10^-14 moles to grams

1 mole of oxygen = 32 grams of oxygen

therefore : 48 * 10^-14 moles of oxygen = ( 32 * (48*10^-14) = 1536*10^-14 grams