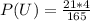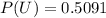Complete Question
A certain WSU curriculum committee consists of 11 members. In a regular meeting last year, seven members of the committee were in favor of a program proposal and the other four rejected it. If the committee members leave the meeting room in random order and each of the first three leaving the room is accosted by a reporter in quest of an interview, then let X be the number of committee members rejecting the proposal among those interviewed.
1. What is the probability that exactly two are from the member favoring the acceptance of the proposal among those interviewed.
Answer:
The value is
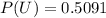
Explanation:
From the question we are told that
The number of member is n = 11
The number of member who are in favor of the project is k = 7
The number of members who rejected the project is h = 4
Generally the number of way of selecting the first three member left out of the 11 members is mathematically represented as
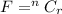
Here r = 3 and C stand for combination , so using a combination calculator we have
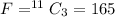
Given that out of the first three members that left 2 of the members accepted the project i.e U = 2
The number of way of selecting the 2 members from the total 7 members that accepted the project is
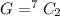
=>
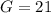
Given that two members out of the first three accepted the project it means that the remaining one person rejected the project, the number of ways of selecting this one person from the 4 that rejected the project is mathematically represented as
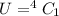
=>
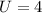
Generally the probability that exactly two are from the member favoring the acceptance of the proposal among those interviewed is mathematically represented as