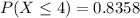Answer:
a
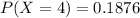
b
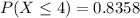
Explanation:
From the question we are told that
The proportion that has outstanding balance is p = 0.20
The sample size is n = 15
Given that the properties of the binomial distribution apply, for a randomly selected number(X) of credit card
Generally the probability of finding 4 customers in a sample of 15 who have "maxed out" their credit cards is mathematically represented as
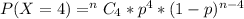
=>
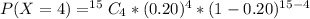
Here C stand for combination
=>
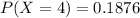
Generally the probability that 4 or fewer customers in the sample will have balances at the limit of the credit card is mathematically represented as
![P(X \le 4) = [ ^(15)C_0 * (0.20)^0 * (1 - 0.20)^(15-0)]+[ ^(15)C_1 * (0.20)^1 * (1 - 0.20)^(15-1)]+\cdots+[ ^(15)C_4 * (0.20)^4 * (1 - 0.20)^(15-4)]](https://img.qammunity.org/2021/formulas/mathematics/college/1mbesp7w38cc5bdhz5qcsymg3dqz6prlk1.png)
=>