Complete Question
The SAT are scored so as to yield a mean of 500 and a standard deviation of 100. These scores are close to being normally distributed. An exclusive club wishes to invite those scoring in the top 5% on the College Boards to join. a. Find percentages of scores that is between 480 and 590. b. What score is required to be invited to join the club? c. What score separates the top 60% of the population from the bottom 40%? What do we call this value? (hint: the score that separates the top 20% of the population from the bottom 80% is called the 80th percentile)
Answer:
a
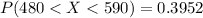
b
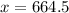
c
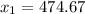
The value is called the
 percentile
percentile
Explanation:
From the question we are told that
The mean is
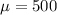
The standard deviation is
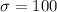
Generally the percentage of the score that are between 480 and 590 is mathematically represented as
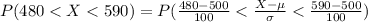
Here

=>
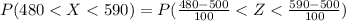
=>
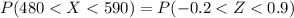
=>

From the z table (reference calculator dot net )
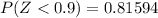
And
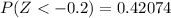
=>
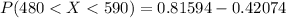
=>
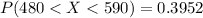
Converting to percent

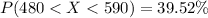
The percentage invited to join the club is the top 5% , this can be mathematically represented as
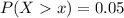
Here x is the score that is within the top 5%
=>
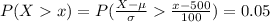
Generally the critical value of 0.05 from the normal distribution table is
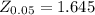
So
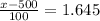
=>
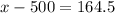
=>
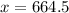
Generally the probability of having a score that separates the top 60% of the population from the bottom 40%
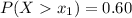
=>

The critical value of 0.60 from the normal distribution table is

So
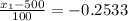
=>
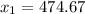
From the hint given we can see that this value is called the
 percentile
percentile