Question

A line goes through the points (7, 3) and (–1, 5). Write the equation of the line in slope-intercept form. Show your work for full credit. (How did you go from those two points to having the equation in slope-intercept form? Or, how did you go form having the equation in point-slope form to slope-intercept form?)

Answer 1

The equation in slope-intercept form is;

`y = -(1)/(4) \cdot x + 4(3)/(4)`

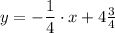
Explanation:

The equation of a straight line in slope and intercept form is given as follows;

y = m·x + c

Where;

m = The slope of the line

c = The y-intercept of the line

The points through which the line passes are;

(7, 3) and (-1, 5), therefore, the slope of the line, m, is given as follows;

`Slope, \, m =(y_(2)-y_(1))/(x_(2)-x_(1))`

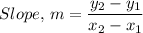
Where (x₁, y₁) = (7, 3) and (x₂, y₂) = (-1, 5), we have;

`Slope, \, m =(5-3)/((-1)-7) = -(1)/(4)`

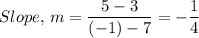
Therefore;

`(y-3)/(x-7) = -(1)/(4)`

The equation in point slope form is therefore;

`y - 3 = -(1)/(4) * (x - 7)`

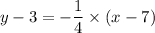
From which we have;

y - 3 = -1/4×(x - 7) = -x/4 + 7/4

y = -x/4 + 7/4 + 3 = -x/4 + 19/4

The equation in slope-intercept form is therefore;

`y = -(1)/(4) \cdot x + 4(3)/(4)`

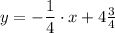
Which can be expressed as follows

y = -0.25·x + 4.75.