This question has the same problem as the other one you shared. Neither cot(32°) = 4/3 nor cos(44°) = 7/9 are true.
But if we indulge the author for a moment, we have from the double angle identity
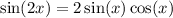
so if x = 32°, then
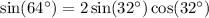
We also have from the Pythagorean identity
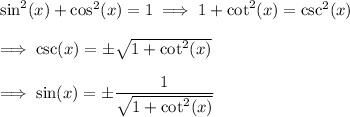
Now, 0° < 32° < 90°, so both sin(32°) and cos(32°) are positive.
If we assume cot(32°) = 4/3 to be true, it follows that
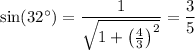
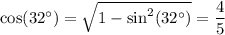
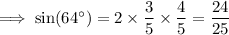
so E is the only correct choice regardless of the baseless assumptions made by the question.