Question

Hello, precalc, need help on finding csc

Answer 1

Recall the double angle identity for cosine:

`\cos(2x) = \cos^2(x) - \sin^2(x) = 1 - 2 \sin^2(x)`

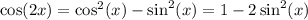
It follows that

`\sin^2(x) = \frac{1 - \cos(2x)}2 \implies \sin(x) = \pm \sqrt{\frac{1-\cos(2x)}2} \implies \csc(x) = \pm \sqrt{\frac2{1-\cos(2x)}}`

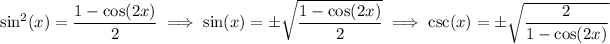
Since 0° < 22° < 90°, we know that sin(22°) must be positive, so csc(22°) is also positive. Let x = 22°; then the closest answer would be C,

`\csc(22^\circ) = \sqrt{\frac2{1-\cos(44^\circ)}} = \sqrt{\frac2{1-\frac5{13}}} = \frac{√(13)}2`

but the problem is that none of these claims are true; cot(32°) ≠ 4/3, cos(44°) ≠ 5/13, and csc(22°) ≠ √13/2...