Question

3

Suppose that the height (in centimeters) of a candle is a linear function of the amount of time (in hours) it has been burning. After 15 hours of burning, a candle
has a height of 22 centimeters. After 27 hours of burning, its height is 19.6 centimeters. What is the height of the candle after 23 hours?

Answer 1

The height of the candle after 23 hours is 20.4 centimeters

Explanation:

Mathematical Modeling

To model a real-life situation, a mathematical model can be built in such a way it accurately represents the variables measured in the system.

This problem requires to build a model for the height of a candle as a linear function of the time it has been burning. If the time is expressed in hours and the height is in centimeters, then the linear function can be written as:

`H(t)=mt+b`

Where m and b are constants we need to find. We are provided two points of reference: After 15 hours of burning, the candle has a height of 22 centimeters. This is the point (15,22).

We also know after 27 hours of burning, the height is 19.6 cm. This is the point (27,19.6). This data is enough to accurately define the function. Let's substitute the first point:

`22=15m+b\qquad\qquad [1]`

Substituting the second point:

`19.6=27m+b\qquad\qquad [2]`

Subtracting [1] - [2]:

`22-19.6=15m-27m`

`\Rightarrow 12m=-2.4`

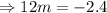
Solving for m:

`m=-2.4/12=-0.2`

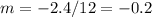
Using this value in [1]:

`22=15(-0.2)+b`

`22=-3+b`

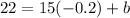
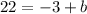
Solving for b:

b=25

The function is now complete:

`H(t)=-0.2t+25`

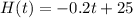
Finally, substitute t=23:

`H(23)=-0.2(23)+25=20.4`

The height of the candle after 23 hours is 20.4 centimeters