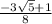Question

find the exact value of cos(A+B) given that sin(A)=-1/2, with angle A in quadrant 4, and sin(B)=1/4, with angle B in quadrant 2

Answer 1

cos(A + B) =
`(-3√(5)+1)/(8)`

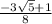
Explanation:

Let us revise some rule of trigonometry

• sin²(x) + cos²(x) = 1

• cos(x + y) = cos(x) cos(y) - sin(x) sin(y)

The sign of the trigonometry functions in the four quadrants

• In the 1st quadrant: sin(x) and cos(x) are positive values

• In the 2nd quadrant: sin(x) is positive value, cos(x) is negative value

• In the 3rd quadrant: sin(x) and cos(x) are negative values

• In the 4th quadrant: sin(x) is negative value, cos(x) is positive value

In the given question

→ Angle A is in the 4th quadrant

∵ sin(A) = -1/2

→ Use the 1st rule above to find cos(A)

∵ (-1/2)² + cos²(A) = 1

∴ 1/4 + cos²(A) = 1

→ Subtract 1/4 from both sides

∴ cos²(A) = 3/4

→ Take square root for both sides

∴ cos(A) = ±√(3/4)

→ In the 4th quadrant cos is a positive value

∴ cos(A) = (√3)/2

→ Angle B is in the 2nd quadrant

∵ sin(B) = 1/4

→ Use the 1st rule above to find cos(B)

∵ (1/4)² + cos²(B) = 1

∴ 1/16 + cos²(B) = 1

→ Subtract 1/16 from both sides

∴ cos²(B) = 15/16

→ Take square root for both sides

∴ cos(B) = ±√(15/16)

→ In the 2nd quadrant cos is a negative value

∴ cos(B) = (-√15)/4

Let us find the exact value of cos(A + B)

→ By using the 2nd rule above

∵ cos(A + B) = cos(A) cos(B) - sin(A) sin(B)

∴ cos(A + B) =
`((√(3))/(2))(-(√(15))/(4))-(-(1)/(2))((1)/(4)) =-(3√(5))/(8)+(1)/(8)`

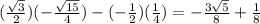
∴ cos(A + B) =
`(-3√(5)+1)/(8)`