Question

You are trying to understand the error surrounding the precipitation estimate that you obtained from one of your rain gages. You have determined that for this gage you have a standard error of 30%. For a precipitation event of 5 inches, what is the probability that the actual event is less than 6.5 inches (please assume a normal distribution) (please also provide the response without a percent sign and in the following numerical format: 00.00)

Answer 1

The probability that the actual event is less than 6.5 inches is 0.9999.

Explanation:

We are given that you have determined that for this gage you have a standard error of 30%.

For a precipitation event of 5 inches, we have to find the probability that the actual event is less than 6.5 inches.

The z-score probability distribution for the normal distribution is given by;

Z =
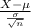`(X-\mu)/((\sigma)/(√(n) ) )` ~ N(0,1)

where,
`\mu` = mean precipitation event = 5 inches

standard error =
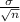`(\sigma)/(√(n) )` = 0.30

Now, the probability that the actual event is less than 6.5 inches is given by = P(X < 6.5 inches)

P(X < 6.5 inches) = P(
`(X-\mu)/((\sigma)/(√(n) ) )` <
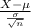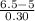`(6.5-5)/(0.30)` ) = P(Z < 5) = 0.9999

The above probability is calculated by looking at the value of x = 5 but in the z table the last value of x is given as 4.40 so we take the area of that value only which has an area of 0.9999.