Question

The cost of a movie ticket in a large city has increased exponentially over the decades since 1953 when records were first kept. A function that models the cost is

C=1.25(1.5)^d
a) Rewrite the equation to give the cost of a movie ticket in terms of y years after 1953 instead of d decades.
b) Use your equation for part a to estimate the cost of a movie ticket in 1996.
c) Open-ended: Do you think your estimate in part b is reasonable

Answer 1

(a)
`C=1.25\cdot (1.5)^(y/10)`

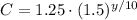
(b) $7.44

(c) Yes.

Explanation:

The exponential function representing the cost of a movie ticket in a large city is as follows:

`C=1.25\cdot (1.5)^(d)`

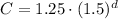
(a)

A decade equals 10 years.

Then for n decades the number of years will be,

y = 10 × n

Then the equation of the cost of a movie ticket in terms of y years after 1953 is as follows:

`C=1.25\cdot (1.5)^(d)`

`=1.25\cdot (1.5)^((10* n)/10)\\=1.25\cdot (1.5)^(y/10)`

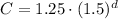
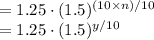
The equation represents the cost of a movie ticket in

(b)

For the year 1953, the value of y is 0.

So, for 1996 the value of y will be, 44.

Compute the cost of a movie ticket in 1996 as follows:

`C=1.25\cdot (1.5)^(y/10)`

`=1.25\cdot (1.5)^(44/10)\\=1.25* 5.9539\\=7.442375\\\approx 7.44`

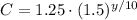
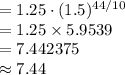
Thus, the cost of a movie ticket in 1996 will be $7.44.

(c)

It is already provided that the cost of a movie ticket in a large city has increased exponentially over the decades since 1953.

So, for the year 1953 the cost of a movie ticket was, $1.25.

And the cost of a movie ticket in 1996 was $7.44.

This value shows an exponential increase in the cost.

Thus, the estimate in part b is reasonable.