Answer:
always True
sometimes true
sometimes true
always true
sometimes true
always true
Explanation:
As product of non-zero rational number and irrational number is irrational,
3x is an irrational number : always True
Take
![x=\sqrt[3]{2}](https://img.qammunity.org/2021/formulas/mathematics/high-school/cqmptw6ei425r1gye49qtzq5olesgb7989.png)
Here,
 is an irrational number.
is an irrational number.
![x^2=(\sqrt[3]{2})^2=2^{(2)/(3) }](https://img.qammunity.org/2021/formulas/mathematics/high-school/3sh7gvfob5rw8tb6li802bedwkhjzo4aqd.png) is also an irrational number
is also an irrational number
Now take

Here,
 is an irrational number.
is an irrational number.
 is a rational number
is a rational number
So,
 is a rational number: sometimes true
is a rational number: sometimes true
Take
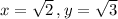
Here,
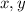 are irrational numbers.
are irrational numbers.
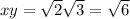 is also an irrational number.
is also an irrational number.
Now take
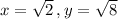
Here,
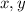 are irrational numbers.
are irrational numbers.
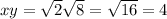 is a rational number.
is a rational number.
So,
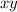 is a rational number: sometimes true
is a rational number: sometimes true
As sum of a rational number and an irrational number is always irrational,
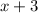 is an irrational number: always true
is an irrational number: always true
Take
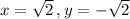
Here,
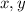 are irrational numbers.
are irrational numbers.
 is a rational number
is a rational number
Now take

Here,
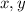 are irrational numbers.
are irrational numbers.
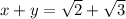 is an irrational number.
is an irrational number.
So,
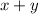 is a rational number: sometimes true
is a rational number: sometimes true
As difference of two irrational numbers is always irrational,
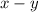 is an irrational number: always true
is an irrational number: always true