Question

Suppose you are an expert on the fashion industry and wish to gather information to compare the amount earned per month by models featuring Liz Claiborne attire with those of Calvin Klein. The following is the amount ($000) earned per month by a sample of 15 Claiborne models:_______.

$3.5 $5.1 $5.2 $3.6 $5.0 $3.4 $5.3 $6.5 $4.8 $6.3 5.8 4.5 6.3 4.9 4.2
The following is the amount ($000) earned by a sample of 12 Klein models.
$4.1 $2.5 $1.2 $3.5 $5.1 $2.3 $6.1 $1.2 $1.5 $1.3 1.8 2.1
1. Find the degrees of freedom for unequal variance test.
2. State the decision rule for 0.01 significance level:
H0:μLC≤μCK; H1:μLC>μCK.
3. Compute the value of the test statistic.

Answer 1

(1) The degrees of freedom for unequal variance test is (14, 11).

(2) The decision rule for the 0.01 significance level is;

• If the value of our test statistics is less than the critical values of F at 0.01 level of significance, then we have insufficient evidence to reject our null hypothesis.

• If the value of our test statistics is more than the critical values of F at 0.01 level of significance, then we have sufficient evidence to reject our null hypothesis.

(3) The value of the test statistic is 0.3796.

Explanation:

We are given that you are an expert on the fashion industry and wish to gather information to compare the amount earned per month by models featuring Liz Claiborne's attire with those of Calvin Klein.

The following is the amount ($000) earned per month by a sample of 15 Claiborne models;

$3.5, $5.1, $5.2, $3.6, $5.0, $3.4, $5.3, $6.5, $4.8, $6.3, $5.8, $4.5, $6.3, $4.9, $4.2 .

The following is the amount ($000) earned by a sample of 12 Klein models;

$4.1, $2.5, $1.2, $3.5, $5.1, $2.3, $6.1, $1.2, $1.5, $1.3, $1.8, $2.1.

(1) As we know that for the unequal variance test, we use F-test. The degrees of freedom for the F-test is given by;

`\text{F}_(_n__1-1, n_2-1_)`

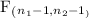
Here,
`n_1` = sample of 15 Claiborne models

`n_2` = sample of 12 Klein models

So, the degrees of freedom = (
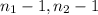`n_1-1, n_2-1`) = (15 - 1, 12 - 1) = (14, 11)

(2) The decision rule for 0.01 significance level is given by;

• If the value of our test statistics is less than the critical values of F at 0.01 level of significance, then we have insufficient evidence to reject our null hypothesis.

• If the value of our test statistics is more than the critical values of F at 0.01 level of significance, then we have sufficient evidence to reject our null hypothesis.

(3) The test statistics that will be used here is F-test which is given by;

T.S. =
`(s_1^(2) )/(s_2^(2) ) * (\sigma_2^(2) )/(\sigma_1^(2) )` ~
`\text{F}_(_n__1-1, n_2-1_)`

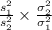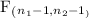
where,
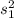`s_1^(2)` = sample variance of the Claiborne models data =
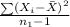`(\sum (X_i-\bar X)^(2) )/(n_1-1)` = 1.007

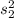`s_2^(2)` = sample variance of the Klein models data =
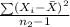`(\sum (X_i-\bar X)^(2) )/(n_2-1)` = 2.653

So, the test statistics =
`(1.007)/(2.653 ) * 1` ~
`\text{F}_(_1_4,_1_1_)`

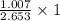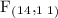
= 0.3796

Hence, the value of the test statistic is 0.3796.