Answer:
V is approximately 1.52 liters
The work done on the gas = 37 J
Step-by-step explanation:
The given information are;
Type of gas = Monoatomic gas
p₁ = 1 atm = 101325 Pa
v₁ = 1 liter = 0.001 m³
T₁ = 373 K
v₂ = 2 liters = 0.002 m³
Final volume = V
For isothermal expansion, we have, Boyle's law given as follows;
p₁×v₁ = p₂×v₂
∴ p₂ = p₁×v₁/(v₂)
p₂ = 1 atm × (1 liter)/(2 liters) = 0.5 atm = 50,662.5 Pa
We have for adiabatic compression, we have;
At V, P = p₂ = 0.5 atm (The gas is cooled at constant pressure) and can be reversed back adiabatically to p₁, v₁
Therefore we have;
![(p_1)/(p_2) = \left [(V)/(v_1) \right ]^\gamma](https://img.qammunity.org/2021/formulas/chemistry/high-school/tbdfthxroybgh0swk3v7xbmznug6qi9gxp.png)
γ = 1.66 for a monoatomic gas, which gives;
![(1 \ atm)/(0.5 \ atm) = \left [(V)/(1 \ liter) \right ]^(1.66)](https://img.qammunity.org/2021/formulas/chemistry/high-school/73fae5at5n6mvzxm34gdxegytl7qirf5f9.png)
![V = 1 \ liter * \sqrt[1.66]{(1 \ atm)/(0.5 \ atm)} = 1 \ liter * \sqrt[1.66]{2} \approx 1.52 \ liters](https://img.qammunity.org/2021/formulas/chemistry/high-school/6j26lrbah3jjijns63qeyiqdf847tibdtl.png)
V ≈ 1.52 liters = 0.00152 m³
The total work done is given given by the following relation;
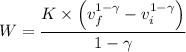
![K = p * v^(\gamma ) = 0.5 * \sqrt[1.66]{2} ^(1.66 ) = 50,662.5 * (0.00152)^(1.66) \approx 1.06\ Pa \cdot m^(4.98)](https://img.qammunity.org/2021/formulas/chemistry/high-school/z2tphkk56cqv5716k5rewe7cq10p8c7t9j.png)
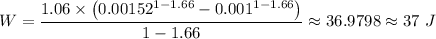
Given that the work done is positive, we have that work is done in the gas
The work done on the gas = 37 J.