Given ratio:
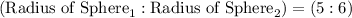
Step-1) Multiply both sides of the ratio by x:
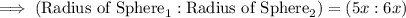
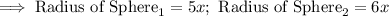
Step-2) Substitute the radiuses of each sphere into the "Volume formula"
Volume of sphere₁ Volume of sphere₂





Step-3) Plug the volume of both spheres in ratio form:
The ratio for the volumes of the two spheres must be in the respective place of the ratio for the radiuses of the two similar spheres. Therefore,
Ratio form:

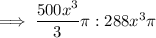
Step-4) Simplify both sides of the ratio:
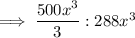
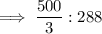
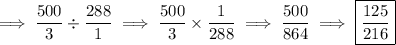
Therefore, the ratio for the volumes of two similar spheres is 125 : 216.