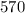Answer:
The appropriate solution is "570". The further explanation is given below
Explanation:
- There's a whole average of 14 committee members of trustees, including 5 out-of-state leaders, 5 in-state senior citizens, 1 out-of-state semi-senior, and 3 semi-senior in-state elderly. Out of those 14 members, 3 members must be chosen. According to the required specifications, the 3 members chosen should also include at least a single in-state member as well as at least 1 longtime leader.
- We may establish the executive committee in two distinct ways, in compliance with us even. One is about choosing the in-state participant from either the five seniors throughout the state, which follows the university's two requirements. As well as the other option is to choose an in-state participant from either the three non-senior in-state students.
- The 2nd incarnation should also be chosen from either the 5 out-of-state leaders throughout the second scenario. Across each circumstance, we can determine the multitude of scenarios, and afterward, the amount of the two can provide the maximum range of things the board can indeed be chosen.
(1)
Choosing the right 1 member out of 5 seniors throughout the state.
The remaining 2 candidates would be chosen from some of the other 13 committee members within a week of choosing 1 member from either the 5 in-state representatives.
So, throughout this case, the number among approaches p is supplied by:
⇒
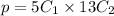
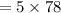
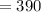
(2)
Choosing the right one person of the legislature out of three non-senior members of the state
In this scenario, as already mentioned, the second participant needs to be chosen from the 5 qualified out-of-state citizens. Currently that we would have chosen 2 members out of 14 members in all, the 3rd member should be chosen out of another leftover 12 people.
Therefore, the amount of forms, throughout this case q, seems to be:
⇒
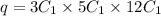
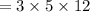
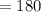
So that the total no. of ways will be:
⇒
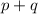
⇒
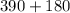
⇒