Question

Certain conditions are set for each race; for example, the age of the horses that could be entered, the gender of the horses that could be entered, and whether the horse has won a prior race or not. Once the conditions are set, owners nominate their eligible horses for the races, and then some of those nominated horses are chosen to run in the race. A random sample of 20 races was selected, and the number of horses nominated for each race is recorded below.

7 13 28 12 16 23 13 49 18 11 9 27 36 18 15 11 32 22 1921
For the data above:_____.
(a) construct an appropriate stem-and-leaf plot to graphically display this data (to do so, type the stems down the left edge of the box, and next to each space over three (3) times, then write the leaves next to the appropriate stems; it is not necessary to draw a line to separate the stems and the leaves:
(b) calculate the mean, median, range, standard deviation, and interquartile range for this data (round all answers to two decimal places):You may do the calculations by hand or with the calculator, partial credit will only be given if correct work is shown:
(c) use the stem-and-leaf plot and appropriate statistics to completely describe the distribution of the number of horses nominated for each race in the sample.

Answer 1

Answer/Step-by-step explanation:

a. To construct a stem-and-leaf plot for the given sample data, 7, 13, 28, 12, 16, 23, 13, 49, 18, 11, 9, 27, 36, 18, 15, 11, 32, 22, 19, 21, first, order the data from the least to the greatest.

7, 9, 11, 11, 12, 13, 13, 15, 16, 18, 18, 19, 21, 22, 23, 27, 28, 32, 36, 49

The plot would like the one shown below:

Stem | Leaf

0 | 7, 9

1 | 1, 1, 2, 3, 3, 5, 6, 8, 8, 9

2 | 2, 3, 7, 8

3 | 2, 36

4 | 9

Key:

13 = 1 | 3

b.

i. Mean = (7 + 9 + 11 + 11 + 12 + 13 + 13 + 15 + 16 + 18 + 18 + 19 + 21 + 22 + 23 + 27 + 28 + 32 + 36 + 49)/20

Mean = 400/20

Mean = 20

ii. Median = average of the 10th and 11th data value

Median = (18 + 18)/2 = 36/2

Median = 18

iii. Range = max value - min value

Range = 49 - 7

Range = 42

iv. Standard deviation for sample data is given as
`s = \sqrt{(1)/(N-1) \sum_(i=1)^N (x_i - \overline{x})^2}`

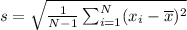
Where,

`\overline{x} = sample mean = 20`

`x_i = each value of the sample data`

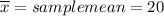
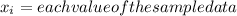
N = total number of values in the sample = 20

Let's solve:

First, calculate
`(x_i - \overline{x})^2` for each data value:

7 => (7 - 20)² = (-13)² = 169

9 => (9 - 20)² = (-11)² = 121

11 => (11 - 20)² = (-9)² = 81

11 => (11 - 20)² = (-9)² = 81

12 => (12 - 20)² = (-8)² = 64

13 => (13 - 20)² = (-7)² = 49

13 => (13 - 20)² = (-7)² = 49

15 => (15 - 20)² = (-5)² = 25

16 => (16 - 20)² = (-4)² = 16

18 => (18 - 20)² = (-2)² = 4

18 => (18 - 20)² = (-2)² = 4

19 => (19 - 20)² = (-1)² = 1

21 => (21 - 20)² = (1)² = 1

22 => (22 - 20)² = (2)² = 4

23 => (23 - 20)² = (3)² = 9

27 => (27 - 20)² = (7)² = 49

28 => (28 - 20)² = (8)² = 64

32 => (32 - 20)² = (12)² = 144

36 => (36 - 20)² = (16)² = 256

49 => (49 - 20)² = (29)² = 841

Next, calculate
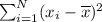`\sum_(i=1)^N (x_i - \overline{x})^2` by summing all results gotten above:

= 169 + 121 + 81+ 81 + 64 + 49 + 49 + 25 + 16 + 4 + 4 + 1 + 1 + 4 + 9 + 49 + 64 + 144 + 256 + 841

= 2,032

Next, find
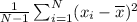`(1)/(N-1) \sum_(i=1)^N (x_i - \overline{x})^2` by dividing the result you have above by (N - 1):

`(2,032)/(N - 1) = (2,032)/(20 - 1)`

`(2,032)/(19) = 106.947368`

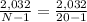
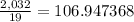
Next, calculate
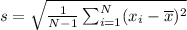`s = \sqrt{(1)/(N-1) \sum_(i=1)^N (x_i - \overline{x})^2}` by finding the square root of the result you have above:

`s = √(106.947)`

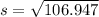
`s = 10.34` (to 2 d.p)

v. Interquartile Range (IQR) = Third Quarter (Q3) - First Quartile (Q1)

Q1 = (12 + 13)/2 = 25/2 = 12.5

Q3 = (23 + 27)/2 = 50/2 = 25

IQR = 25 - 12.5

IQR = 12.5

c. The distribution of the number of horses nominated for each race in the sample is slightly down-skewed. This indicates that most of lower number of horses nominated for each race in the sample chosen are more common. Most of the data values are below the mean value of 20. Also, the median shows the median number of horses selected to be 18, indicating a lower number.

With the distribution having a range value of 42, extreme value such as 49, seem to be an outlier, as it does not reflect the typical number of horses selected in each race, which are mostly lower.