Answer:
a) dx = v₀o cos θ dt , dy = (v_{oy} - g t) dt
b) dx / dt = v₀ₓ e^{- (\gamma/ m) t} , dv_y/dt - γ/m v_y + g =0
Step-by-step explanation:
For this exercise we will use Newton's second law on each axis
F = m a
F = m d²x / dt²
let's use trigonometry for the components of the initial velocity
cos θ = v₀ₓ / v₀
sin θ = v_{oy} / v₀
v₀ₓ = vo cos θ
v_{oy} = v₀ sin θ
now we will work on each component
a) in this case there is no air resistance
X axis
Fₓ = 0
0 = m d²x / dt²
0 = m dv / dt
we integrate once
m dv = 0
m (vf- vo) = 0
v_f = v₀
we use the definition of velocity
v = dx / dt
vₓ = dx / dt
dx = v₀ₓ dt
dx = v₀o cos θ dt
we integrate once
x_f-x₀ = vₓ cos θ (t-0)
y axis
in this case the force is the weight of the body
F = W = - mg
F = m a
-m g = ma
a = -g
we use the relationship between acceleration and velocity
a = dv / dt
dv / dt = -g
dv = -g dt
we integrate
(v_y-v_{oy}) = -g (t-0)
v_y = v_{oy} - g t
now we love the relationship
v = dy / dt
dy / dt = v_{oy} - g t
dy = (v_{oy} - g t) dt
we integrate
y- y_o = v_{oy} - ½ g t²
y = y_o + v₀ sin tea t - ½ g t²
B) in this case there is air resistance, we will assume that in the two axes
x-axis) resistance always opposes movement
fr = - g v
∑ F = m aₓ
- γ vx = m dvₓ / dt
dvₓ / vₓ = - γ/m dt
ln vₓ / ln v₀ₓ = - γ/m (t-0)
vₓ = v₀ₓ
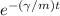
let's use the relationship between speed and distance
dx / dt = v₀ₓ e^{- (\gamma/ m) t}
dx = v₀ₓ e^{- (\gamma/ m) t} dt
Y axis
∑ F = m a_y
fr- W = m a_y
γ v_y - m g = m a_y
a_y = γ/m v_y - g
d v_y / dt = (γ /m v_y - g)
dv_y/dt - γ/m v_y + g =0
in this equation differences for the initial time the velocities vo = vo sin θ