Question

A group of students has conducted an experiment to investigate which enzyme (cellulase or pectinase) or combination of the two enzymes would produce the most apple juice from small chunks of apples. They mixed the specified amount of each enzyme with 50 grams of apple sauce and then filtered the apple juice for 15 minutes into a graduated cylinder. They repeated the control and experimental groups for a total of 5 trials each. The students' results are given below. Table 5. Apple Juice Production Amount of Apple Juice Produced from Apple Sauce (mL) 10 drops of cellulase 5 drops of pectinase+5 drops of cellulase 10 10 drops of 10 drops of water pectinase 12.5 0.71 Mean of 5 trials St. Dev. SEx 95% CI 3.5 0.61 0.50 0.82

Calculate the standard error of the mean (SE) and 95% confidence interval for the control and experimental groups.

Answer 1

Explained below.

Explanation:

The information provided is:

Mean Standard Deviation

10 drops of water 4 0.61

10 drops of cellulase 3.5 0.50

10 drops of pectinase 12.5 0.71

5 drops of pectinase 10 0.82

+ 5 drops of cellulase

• Calculate the standard error of the mean (SE) and 95% confidence interval for the group "10 drops of water" as follows:

`SE=(s)/(√(n))=(0.61)/(√(10))=0.192899\approx 0.1929`

`CI=\bar x\pm t_(\alpha/2)* SE\\\\=4\pm 2.262* 0.1929\\\\=(3.5636602,\ 4.4363398)\\\\\approx (3.56, 4.44)`

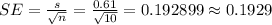
• Calculate the standard error of the mean (SE) and 95% confidence interval for the group "10 drops of cellulase " as follows:

`SE=(s)/(√(n))=(0.50)/(√(10))=0.1581139\approx 0.1581`

`CI=\bar x\pm t_(\alpha/2)* SE\\\\=3.5\pm 2.262* 0.1581\\\\=(3.1423778,\ 3.8576222)\\\\\approx (3.14, 3.86)`

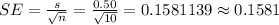
• Calculate the standard error of the mean (SE) and 95% confidence interval for the group "10 drops of pectinase" as follows:

`SE=(s)/(√(n))=(0.71)/(√(10))=0.2245217\approx 0.2245`

`CI=\bar x\pm t_(\alpha/2)* SE\\\\=12.5\pm 2.262* 0.2245\\\\=(11.992181,\ 13.007819)\\\\\approx (11.99, 13.01)`

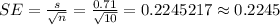
• Calculate the standard error of the mean (SE) and 95% confidence interval for the group "5 drops of pectinase + 5 drops of cellulase" as follows:

`SE=(s)/(√(n))=(0.82)/(√(10))=0.25930677\approx 0.2593`

`CI=\bar x\pm t_(\alpha/2)* SE\\\\=10\pm 2.262* 0.2593\\\\=(9.4134634,\ 10.5865366)\\\\\approx (9.41, 10.59)`

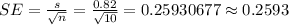
The critical value of t is computed using the t-table for 95% confidence level and (n - 1) 9 degrees of freedom.