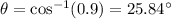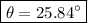Question

the bob of a pendulum 0.4m long is 4cm higher at the top of its swing than its bottom. Find the angle of swing on each side of the vertical​

Answer 1

`\theta=25.84^\circ`

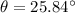
Explanation:

Pendulum

The length of the pendulum is 0.4 m or 40 cm. When swinging, it reaches the top height of 4 cm from the bottom. The geometric construction of this situation is shown in the image below.

The right triangle is formed by the length of the pendulum (40 cm), its horizontal displacement, and the vertical height projected by the pendulum.

This last distance is calculated subtracting the total length of the pendulum and the vertical displacement reached in its higher position.

We need to calculate the angle θ, for which we'll use the cosine since we know the adjacent leg and the hypotenuse:

`\displaystyle \cos\theta=(36)/(40)=0.9`

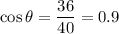
The angle is

`\theta=\cos^(-1)(0.9)=25.84^\circ`

`\boxed{\theta=25.84^\circ}`