Answer:
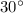 .
.
Explanation:
Let
 denote the unknown angle of elevation. Let
denote the unknown angle of elevation. Let
 denote the height of the tower.
denote the height of the tower.
Refer to the diagram attached. In this diagram,
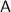 denotes the top of the tower while
denotes the top of the tower while
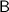 denote the base of the tower;
denote the base of the tower;
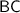 and
and
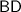 denote the shadows of the tower when the angle of elevation of the sun is
denote the shadows of the tower when the angle of elevation of the sun is
 and
and
 , respectively. The length of segment
, respectively. The length of segment
 is
is
 ;
;
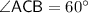 ,
,
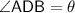 , and
, and
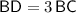 ..
..
Note that in right triangle
 , segment
, segment
 (the tower) is opposite to
(the tower) is opposite to
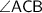 . At the same time, segment
. At the same time, segment
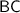 (shadow of the tower when the angle of elevation of the sun is
(shadow of the tower when the angle of elevation of the sun is
 ) is adjacent to
) is adjacent to
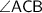 .
.
Thus, the ratio between the length of these two segments could be described with the tangent of
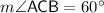 :
:
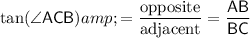 .
.
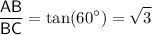 .
.
The length of segment
 is
is
 . Rearrange this equation to find the length of segment
. Rearrange this equation to find the length of segment
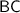 :
:
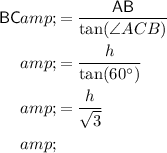 .
.
Therefore:
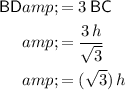 .
.
Similarly, in right triangle
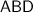 , segment
, segment
 (the tower) is opposite to
(the tower) is opposite to
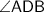 . Segment
. Segment
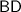 (shadow of the tower, with
(shadow of the tower, with
 as the angle of elevation of the sun) is adjacent to
as the angle of elevation of the sun) is adjacent to
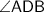 .
.
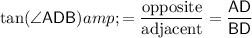 .
.
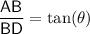 .
.
Since
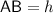 while
while
 :
:
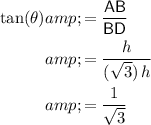 .
.
Therefore:
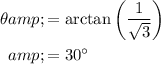 .
.
In other words, the angle of elevation of the sun at the time of the longer shadow would be
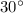 .
.