Question

Please please help!!

Answer 1

The explicit formula is
`a_(n)` = - 13 - 7n

Explanation:

Let us at first find the type of the sequence

∵ The terms are - 20, - 27, - 34, - 41, ............

→ Find the difference between each to consecutive terms

∵ - 27 - (- 20) = - 27 + 20 = - 7

∵ - 34 - (- 27) = - 34 + 27 = - 7

∵ - 41 - (- 34) = - 41 + 34 = - 7

→ There is a constant difference between each two consecutive terms

∴ The sequence is Arithmetic

→ The explicit formula of the nth term of the arithmetic sequence is

• 
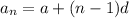  `a_(n)=a+(n-1)d`, where
• a is the first term
• d is the constant difference
• n is the position of the number

∵ a = - 20

∵ d = -7

∴
`a_(n)=-20+(n-1)(-7)`

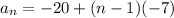
→ Simplify it

∴
`a_(n)` = - 20 + (-7)(n) - (-7)(1)

∴
`a_(n)` = - 20 + (-7n) - (-7)

∴
`a_(n)` = - 20 - 7n + 7

→ Add the like terms

∴
`a_(n)` = (- 20 + 7) - 7n

∴
`a_(n)` = - 13 - 7n

The explicit formula is
`a_(n)` = - 13 - 7n