Question

AP CAL AB HELP!

A plane flying with a constant speed of 14 km/min passes over a ground radar station at an altitude of 11 km and climbs at an angle of 25 degrees. At what rate is the distance from the plane to the radar station increasing 4 minutes later?
The distance is increasing at equation editorEquation Editor____ km/min.

Answer 1

`(dc)/(dt)\approx13.8146\text{ km/min}`

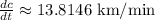
Explanation:

We know that the plane travels at a constant speed of 14 km/min.

It passes over a radar station at a altitude of 11 km and climbs at an angle of 25°.

We want to find the rate at which the distance from the plane to the radar station is increasing 4 minutes later. In other words, if you will please refer to the figure, we want to find dc/dt.

First, let's find c, the distance. We can use the law of cosines:

`c^2=a^2+b^2-2ab\cos(C)`

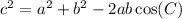
We know that the plane travels at a constant rate of 14 km/min. So, after 4 minutes, the plane would've traveled 14(4) or 56 km So, a is 56, b is a constant 11. C is 90+20 or 115°. Substitute:

`c^2=(56)^2+(11)^2-2(56)(11)\cos(115)`

Evaluate:

`c^2=3257-1232\cos(115)`

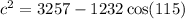
Take the square root of both sides:

`c=√(3257-1232\cos(115))`

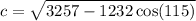
Now, let's return to our law of cosines. We have:

`c^2=a^2+b^2-2ab\cos(C)`

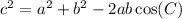
We want to find dc/dt. So, let's take the derivative of both sides with respect to t:

`(d)/(dt)[c^2]=(d)/(dt)[a^2+b^2-2ab\cos(C)]`

Since our b is constant at 11 km, we can substitute this in:

`(d)/(dt)[c^2]=(d)/(dt)[a^2-(11)^2-2a(11)\cos(C)]`

Evaluate:

`(d)/(dt)[c^2]=(d)/(dt)[a^2-121-22a\cos(C)]`

Implicitly differentiate:

`2c(dc)/(dt)=2a(da)/(dt)-22\cos(115)(da)/(dt)`

Divide both sides by 2c:

`(dc)/(dt)=(2a(da)/(dt)-22\cos(115)(da)/(dt))/(2c)`

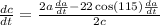
Solve for dc/dt. We already know that da/dt is 14 km/min. a is 56. We also know c. Substitute in these values:

`(dc)/(dt)=(2(56)(14)-22\cos(115)(14))/(2√(3257-1232\cos(115)))`

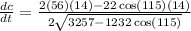
Simplify:

`(dc)/(dt)=(1568-308\cos(115))/(2√(3257-1232\cos(115)))`

Use a calculator. So:

`(dc)/(dt)\approx13.8146\text{ km/min}`

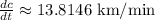
And we're done!