An equation for the depreciation of a car is given by y = A(1 – r)t , where y = current value of the car, A = original cost, r = rate of depreciation, and t = time, in years. Th…

Question

asked Feb 17, 2021 95.9k views

1 Answer

Jackhab · Answer 1 · 2021-02-21T15:27:29+0000

Answer:

D; 6.6 years.

Explanation:

We know that the equation for the depreciation of the car is:

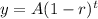
y=A(1-r)^t

Where y is the current cost, A is the original cost, r is the rate of depreciation, and t is the time, in years.

We are told that the value of the car now is half of what it originally cost. So:

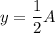
$\displaystyle y=(1)/(2)A$

Substitute this for y:

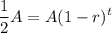
$\displaystyle (1)/(2)A=A(1-r)^t$

We also know that the rate of depreciation is 10% or 0.1. Substitute 0.1 for r:

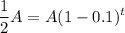
$\displaystyle (1)/(2)A=A(1-0.1)^t$

So, let's solve for t. Divide both sides by A:

$\displaystyle (1)/(2)=(1-0.1)^t$

Subtract within the parentheses:

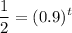
$\displaystyle (1)/(2)=(0.9)^t$

Take the natural log of both sides:

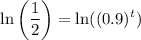
$\displaystyle \ln\left((1)/(2)\right)=\ln((0.9)^t})$

Using the properties of logarithms, we can move the t to the front:

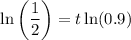
$\displaystyle \ln\left((1)/(2)\right)=t\ln(0.9)$

Divide both sides by ln(0.9):

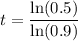
$\displaystyle t=(\ln(0.5))/(\ln(0.9))$

Use a calculator. So, the car is approximately:

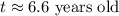
$t\approx6.6\text{ years old}$

Our answer is D.

And we're done!