Question

One operator is holding a laser pointer at a height of 9 feet whose beam is reflected on a horizontal reflecting surface at a point 8 feet away from the pointer. A wall is 7 feet away from where the beam is reflected. When the y-axis is placed as the vertical line of the pointer and the x axis placed at the same height of the reflection point, the absolute value equation that represents the situation is shown below. How high (in feet) will the laser beam impact the wall 7 feet from the reflection point?

f(x)=9/8|x-8|

Answer 1

The height (in feet) at which the laser will impact the wall is 6.75 feet

Explanation:

The given parameters are;

The height from which the laser beam operator is holding the laser = 9 feet

The horizontal distance away from the pointer the beam is reflected = 8 feet

Given that we have;

`f(x) = (9)/(8) * \left | x - 8\right | = y`

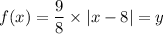
When x = 8, the point of reflection, the height, f(x) is given as follows;

`f(x) = (9)/(8) * \left | 8 - 8\right | = 0`

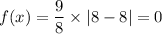
When x = 7, the point of reflection, the height, f(x) is given as follows;

`f(x) = (9)/(8) * \left | 7 - 8\right | = (9)/(8)`

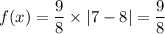
Therefore, given that the point of reflection is at an elevation of 0 relative to the 9 feet of the laser source (pointer), by tan rule, we have;

`tan(\theta) = (Opposite \ side)/(Adjacent \ side) =(9)/(8) = (h)/(7)`

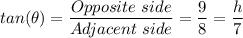
Where;

h = The height at which the laser meets the wall

`h = (9 * 7)/(8) =7.875`

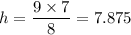
Given that the wall the laser meets is at the point x with elevation 9/8, the height, y, at which the laser meets the wall is therefore;

`y = (9 * 7)/(8) - (9)/(8) = (54)/(8) = 6.75 \ feet`

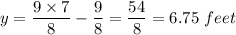
The height (in feet) at which the laser will impact the wall = 6.75 feet.