Answer:
The length of segment AB is 10
Explanation:
The distance formula is d=
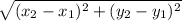
With the points (-4,1) and (2,9) you know that
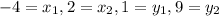
Now you put the numbers into the distance formula
d=
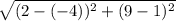
(2-(-4) turns into (2+4) because two negatives equal a positive.
After adding and subtracting you get d=
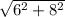
You then square
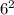 and
and
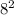 to get
to get
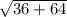
After adding 34+64 you get
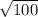 , which is 10
, which is 10
So the length of segment AB is 10