Answer:
11 music lessons.
Explanation:
We know that membership costs $165 and members pay $25 per music lesson.
So, we can write the following expression:
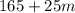
The 165 represents the one-time membership fee and the 25m represents the cost for m music lessons.
We know that non-members pay no membership fee but their cost per lesson is $40. So:
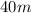
Represents the cost for non-members for m music lessons.
We want to find how many music lessons would have to be taken for the cost to be the same for both members and non-members. So, we can set the expressions equal to each other:
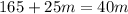
And solve for m. Let's subtract 25m from both sides:
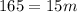
Now, divide both sides by 15:

So, at the 11th music lesson, members and non-members will pay the same.
Further Notes:
This means that if a person would only like to take 10 or less lessons, the non-membership is best because there is no initial fee.
However, if a person would like to take 12 or more lessons, than the membership is best because the membership has a lower cost per lesson than the non-membership.
And we're done!