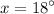Question

If sin(2x)sin(3x)=cos(2x)cos(3x), then find the smallest positive value of x. Express your answer in degrees, but without the degree symbol.

Answer 1

`x=18\textdegree`

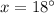
Explanation:

We are given the equation:

`\sin(2x)\sin(3x)=\cos(2x)\cos(3x)`

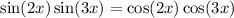
And we want to find the smallest positive value of x such that it makes the equation true.

We can rewrite our equations as:

`\displaystyle \cos(2x)\cos(3x) - \sin(2x)\sin(3x) = 0`

Recall that:

`\displaystyle \cos (\alpha + \beta) = \cos \alpha\cos-\sin\alpha\sin\beta`

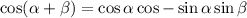
Therefore, by letting α = 2x and β = 3x, we obtain:

`\displaystyle \begin{aligned} \cos(2x)\cos(3x) - \sin(2x)\sin(3x) & = \cos (2x + 3x) \\ \\ &= \cos 5x \end{aligned}`

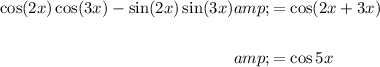
Hence:

`\displaystyle \cos 5x = 0`

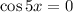
Recall the Unit Circle. The smallest angle value for which cosine equals 0 is cos(90°). Thus:

`\displaystyle 5x = 90^\circ`

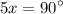
Therefore:

`\displaystyle x = 18^\circ`

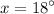
In conclusion:

`\displaystyle x = 18^\circ`