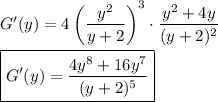Answer:
G'(y) = 4y^7(y+4)/(y+2)^5
Explanation:
Work it a piece at a time.
Define z = y^2/(y+2). Then your derivative is found from the power rule as ...
G = z^4
G' = 4z^3·z'
Now, define z = u/v. Then your derivative is found using the quotient rule:
z' = (vu' -uv')/v^2 = ((y+2)(2y) -(y^2)(1))/(y+2)^2
Putting this together we have ...