Question

Astronomers observe a spectral analysis of a distant star where a particular element has a spectral line with a wavelength of 663 nm. In the laboratory, the same element has a spectral line with a wavelength of 645 nm.

a. How fast is the star moving, and in what direction is it moving?

b. The same element on Earth’s surface is observed from a space shuttle orbiting at 7800 m/s,
350 km above Earth. Is the same shift in the spectral line seen from the space shuttle? Why or why not?

Answer 1

(a). The velocity of star is
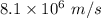`8.1*10^(6)\ m/s` and the direction of star toward the earth.

(b). The shift is 0.0168 nm.

Step-by-step explanation:

Given that,

Wavelength of spectral line = 663 nm

Wavelength of spectral line in lab = 645 nm

(a). We need to calculate the velocity

Using doppler's effect

`\Delta \lambda=(v)/(c)\lambda`

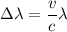
Where,
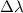`\Delta\lambda`= change in wavelength

v = velocity

c = speed of light

Put the value into the formula

`663-645=(v)/(3*10^(8))*663`

`v=(3*10^(8)(663-645))/(663)`

`v=8144796.38\ m/s`

`v=8.1*10^(6)\ m/s`

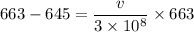
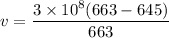
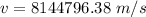
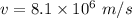
The direction of star toward the earth.

(b). Speed = 7800 m/s

We need to calculate the shift

Using formula of shift

`\Delta \lambda=\lambda(\sqrt{(1+(v)/(c))/(1-(v)/(c))}-1)`

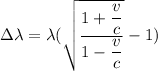
Put the value into the formula

`\Delta \lambda=645*(\sqrt{(1+(7800)/(3*10^(8)))/(1-(7800)/(3*10^(8)))}-1)`

`\Delta\lambda=0.0168\ nm`

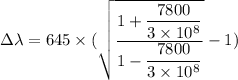
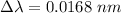
This shift is small compare to the the movement of Earth around the sun.

Hence, (a). The velocity of star is
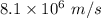`8.1*10^(6)\ m/s` and the direction of star toward the earth.

(b). The shift is 0.0168 nm.