Question

The center of the Hubble space telescope is 6940 km from Earth’s center. If the gravitational force between Earth and the telescope is 9.21 × 104 N, and the mass of Earth is 5.98 × 1024 kg, what is the mass of the telescope? Round the answer to the nearest whole number.

Answer 1

11121.19 kg

Step-by-step explanation:

Given that,

the gravitational force between Earth and the telescope is
`9.21* 10^4\ N`

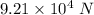
Mass of the Earth is
`5.98* 10^(24)\ kg`

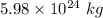
The center of the Hubble space telescope is 6940 km from Earth’s center.

We know that, the force of gravity is given by the formula as follows :

`F=(GmM)/(r^2)`

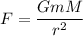
m is mass of telescope and M is mass of Earth

So,

`m=(Fr^2)/(GM)\\\\m=(9.21* 10^4* (6940* 10^3)^2)/(6.67* 10^(-11)* 5.98* 10^(24))\\\\m=11121.19\ kg`

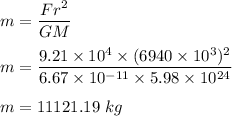
So, the mass off the telescope is 11121.19 kg