Question

Graph the line y = kx +1 if it is known that the point M belongs to it: M(1,3)

Answer 1

Graph the points, (2, -7), (1, -3)

Explanation:

I did it in rsm xD

Answer 2

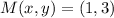`M(x,y) = (1,3)` belongs to the line
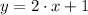`y = 2\cdot x +1`. Please see attachment below to know the graph of the line.

Explanation:

From Analytical Geometry we know that a line is represented by this formula:

`y=k\cdot x + b`

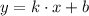
Where:

`x` - Independent variable, dimensionless.

`y` - Dependent variable, dimensionless.

`k` - Slope, dimensionless.

`b` - y-Intercept, dimensionless.

If we know that
`b = 1`,
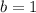`x = 1` and
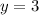`y = 3`, then we clear slope and solve the resulting expression:

`k = (y-b)/(x)`

`k = (3-1)/(1)`

`k = 2`

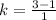
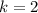
Then, we conclude that point
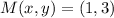`M(x,y) = (1,3)` belongs to the line
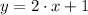`y = 2\cdot x +1`, whose graph is presented below.