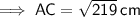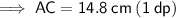Answer:
AC = 14.8 cm (1 dp)
Explanation:
Cosine rule
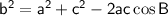
(where a, b and c are the sides, and B is the angle opposite side b)
Given:
- a = 10 cm
- c = 7 cm
- B = 120°
- b = AC
Substituting the given values into the formula and solving for b:
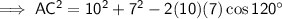
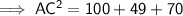
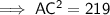
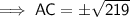
As length is positive,