Answer:
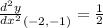
Explanation:
We have the equation:
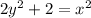
And we want to find d²y/dx² at the point (-2, -1).
So, let's take the derivative of both sides with respect to x:
![(d)/(dx)[2y^2+2]=(d)/(dx)[x^2]](https://img.qammunity.org/2021/formulas/mathematics/high-school/te3zde1u4cxq7iugbpv3ku0v6qllncc7da.png)
On the left, let's implicitly differentiate:
![4y(dy)/(dx)=(d)/(dx)[x^2]](https://img.qammunity.org/2021/formulas/mathematics/high-school/1ls50on7h8yo4926ptc0p7dkvhi47pfg8f.png)
Differentiate normally on the left:
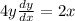
Solve for the first derivative. Divide both sides by 4y:
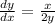
Now, let's take the derivative of both sides again:
![(d)/(dx)[(dy)/(dx)]=(d)/(dx)[(x)/(2y)]](https://img.qammunity.org/2021/formulas/mathematics/high-school/c39locie5actoiid9cp6xdb5k06ee3or5q.png)
We will need to use the quotient rule:
![(d)/(dx)[f/g]=(f'g-fg')/(g^2)](https://img.qammunity.org/2021/formulas/mathematics/high-school/j0vrn6fqgxs0e1tskact5gg0ydwxpids0u.png)
So:
-x(d)/(dx)[(2y)])/((2y)^2)](https://img.qammunity.org/2021/formulas/mathematics/high-school/1ycp0tqxp1fh1eqawejunqpre1t5vr8jta.png)
Differentiate:
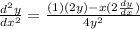
Simplify:
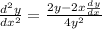
Substitute x/2y for dy/dx. This yields:
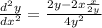
Simplify:
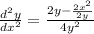
Simplify. Multiply both the numerator and denominator by 2y. So:
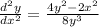
Reduce. Therefore, our second derivative is:
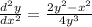
We want to find the second derivative at the point (-2, -1).
So, let's substitute -2 for x and -1 for y. This yields:

Evaluate:
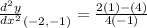
Multiply:
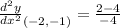
Subtract:
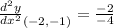
Reduce. So, our answer is:
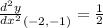
And we're done!