Answer:
22.5° and 67.5°
Explanation:
The sum of complementary angles equal 90°.
Given that one of the complementary angles is 3 times larger than the other, let "x" represent the other angle.
Thus, the following expression can be written to represent this case:

Solve for x
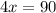
Divide both sides by 4
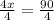
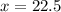
The measure of the complementary angles are:
x = 22.5°
3x = 3(22.5) = 67.5°