Question

Simplify- 4c^2-36/8c^2-24c/12c+36/2c^2-6c
pls help :)

Answer 1

d

Explanation:

separate the 2 divisions and simplify each , that is

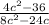`(4c^2-36)/(8c^2-24c)` ← factor numerator/ denominator

=
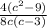`(4(c^2-9))/(8c(c-3))` ← factor difference of squares on numerator

=
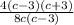`(4(c-3)(c+3))/(8c(c-3))` ← cancel (c - 3) and 4/8 on numerator/ denominator

=
`(c+3)/(2c)`

---------------------------------------------------

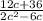`(12c+36)/(2c^2-6c)` ← factor numerator/ denominator

=
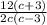`(12(c+3))/(2c(c-3))` ← cancel 12 and 2 on numerator/ denominator

=
`(6(c+3))/(c(c-3))`

----------------------------------------------------------

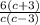
to divide the top fraction by the lower fraction

leave top fraction, change division to multiplication, turn lower fraction upside down.

`(c+3)/(2c)` ×
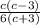`(c(c-3))/(6(c+3))` ← cancel (c + 3) and c on numerator/ denominator

=
`(c-3)/(2(6))`

=
`(c-3)/(12)` → d

Answer 2

`\displaystyle ((4c^2-36)/(8c^2-24c))/((12c+36)/(2c^2 -6c))\\\\\\=\left((4c^2 -36)/(8c^2 -24c)\right) \cdot \left((2c^2 -6c)/(12c+36)\right)\\\\\\=\left[(4(c^2 -9))/(8(c^2-3))\right]\cdot\left[(2(c^2-3))/(12(c+3))\right]\\\\\\=(8(c^2-3^2))/(8 \cdot 12(c+3))\\\\\\=((c+3)(c-3))/(12(c+3))\\\\\\=(c-3)/(12)`

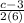
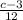`\text{Hence the answer is d.}`