Question

Use the Law of Sines to find the missing angle of the triangle.

Find m∠B to the nearest tenth.

Answer 1

m∠B = 70.0° (nearest tenth)

Explanation:

Sine Rule for Angles

`\sf (\sin A)/(a)=(\sin B)/(b)=(\sin C)/(c)`

(where A, B and C are the angles and a, b and c are the sides opposite the angles)

Given:

• a = 13
• c = 19
• A = 40°

Substituting the given values into the formula to find m∠C:

`\implies \sf (\sin 40^(\circ))/(13)=(\sin C)/(19)`

`\implies \sf \sin C=(19\sin 40^(\circ))/(13)`

`\implies \sf C=\sin^(-1)\left((19\sin 40^(\circ))/(13)\right)`

`\implies \sf m \angle C=69.96086904^(\circ)`

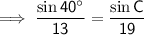
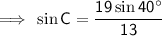
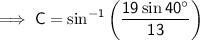
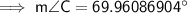
Interior angles of a triangle sum to 180°

`\implies \sf m \angle A+ m \angle B+m \angle C=180^(\circ)`

`\implies \sf 40^(\circ) + m \angle B+69.960...^(\circ)=180^(\circ)`

`\implies \sf m \angle B=70.03913...^(\circ)`

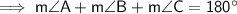
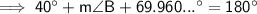
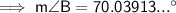
Therefore, m∠B = 70.0° (nearest tenth)