Question

For many purposes we can treat ammonia NH3 as an ideal gas at temperatures above its boiling point of −33.°C.

Suppose the temperature of a sample of ammonia gas is lowered from 15.0°C⁢ to −25.0°C, and at the same time the pressure is changed. If the initial pressure was 0.79kPa and the volume increased by 60.0%, what is the final pressure? Round your answer to 2 significant digits.

Answer 1

Approximately
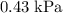`0.43\; \rm kPa` (rounded to two significant figures.)

Step-by-step explanation:

Let
`P_0`.
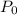`V_0`, and
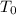`T_0` denote the initial pressure, volume, and temperature of this sample. Let
`P_1`.
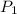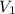`V_1`, and
`T_1` denote the final pressure, volume, and temperature of this sample.

Convert the two temperatures to degrees Kelvins:

`T_0 = 15.0 + 273.15 = 288.15\; \rm K`.

`T_1 = (-25.0) + 273.15 = 248.15\; \rm K`.

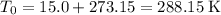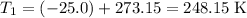Based on the assumption that the ammonia sample here is an ideal gas, it should satisfy the ideal gas equation:

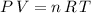`P\, V = n\, R \, T`, where:

• 
  `P` is the pressure of this gas.
• 
  `V` is the volume of this gas.
• 
  `n` is the number of moles of gas particles in this sample.
• 
  `R` is the ideal gas constant, and
• 
  `T` is the temperature of this gas in degrees Kelvins.

The value of the ideal gas constant,
`R`, should stay the same during this change.

On the other hand, assume that this sample did not leak during this change. Hence, the number of moles of gas particles in the sample,
`n`, should also stay the same during this change.

Therefore:

`\displaystyle (P_0\, V_0)/(T_0) = n\, R`.

`\displaystyle (P_1\, V_1)/(T_1) = n\, R`.

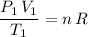Combine these two equations to obtain:

`\displaystyle (P_0\, V_0)/(T_0) = (P_1\, V_1)/(T_1)`.

Rearrange this equation and solve for
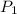`P_1`, the final pressure of this sample:

`P_1 = \displaystyle (P_0\, V_0\, T_1)/(T_0\, V_1) = (P_0\, T_1)/(T_0) \cdot \left((V_0)/(V_1)\right)`.

The question stats that the Initial pressure of this sample is
`P_0 = 0.79\; \rm kPa`.

On the other hand, volume "increased by
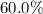`60.0\%`" means that the final volume would be
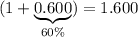`(1 + \underbrace{0.600}_(60\%)) = 1.600` times the initial volume. Therefore:

`\displaystyle (V_0)/(V_1) = (V_0)/((1 + 0.600)\, V_0) = (1)/(1.600)`.

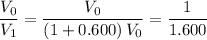Solve for the final pressure of this sample,
`P_1`:

`\begin{aligned}P_1 &= (P_0\, T_1)/(T_0) \cdot \left((V_0)/(V_1)\right) \\ &= (0.79\; \rm kPa * 248.15\; \rm K)/(288.15\; \rm K) * (1)/(1.600) \approx 0.43\;\rm kPa\end{aligned}`.

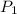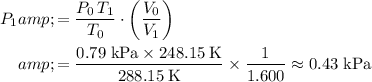(Rounded to two significant digits.)