Question

Explain the steps to finding the vertex of g(x) = 3x2 + 12x + 15

Answer 1

The vertex of this parabola,
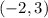`(-2, 3)`, can be found by completing the square.

Explanation:

The goal is to express this parabola in its vertex form:

`g(x) = a\, (x - h)^2 + k`,

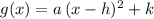where
`a`,
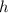`h`, and
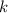`k` are constants. Once these three constants were found, it can be concluded that the vertex of this parabola is at
`(h,\, k)`.

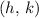The vertex form can be expanded to obtain:

`\begin{aligned}g(x)&= a\, (x - h)^2 + k \\ &= a\, \left(x^2 - 2\, x\, h + h^2\right) + k = a\, x^2 - 2\, a\, h\, x + \left(a\,h^2 + k\right)\end{aligned}`.

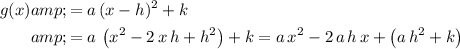Compare that expression with the given equation of this parabola. The constant term, the coefficient for
`x`, and the coefficient for
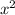`x^2` should all match accordingly. That is:

`\left\lbrace\begin{aligned}& a = 3 \\ & -2\,a\, h = 12 \\& a\, h^2 + k = 15\end{aligned}\right.`.

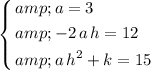The first equation implies that
`a` is equal to
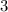`3`. Hence, replace the "
`a\!`" in the second equation with
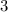`3\!` to eliminate
`\! a`:

`(-2* 3)\, h = 12`.

`h = -2`.

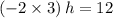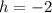Similarly, replace the "
`a`" and the "
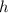`h`" in the third equation with
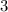`3` and
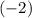`(-2)`, respectively:

`3 * (-2)^2 + k = 15`.

`k = 3`.

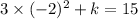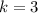Therefore,
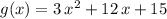`g(x) = 3\, x^2 + 12\, x + 15` would be equivalent to
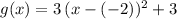`g(x) = 3\, (x - (-2))^2 + 3`. The vertex of this parabola would thus be:

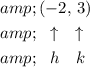`\begin{aligned}&(-2, \, 3)\\ &\phantom{(}\uparrow \phantom{,\,} \uparrow \phantom{)} \\ &\phantom{(}\; h \phantom{,\,} \;\;k\end{aligned}`.